8.Sınıf Eşlik ve Benzerlik Konu Anlatımı ‘nı PDF Olarak indirmek için Aşağıdaki Linkleri kullanabilirsiniz.
MEB BAĞLANTISINI KULLANANLAR AŞAĞIDAKİ LİNKTEN İNDİREBİLİRSİNİZ.
ÜÇGENLERDE EŞLİK
# İki üçgenin karşılıklı kenarının uzunlukları ve açılarının ölçüleri birbirine eşit ise bu üçgenler eş üçgenlerdir.
# İki üçgenin eşliği “≅” sembolü ile gösterilir. Sembolle gösterirken eş olan açılar aynı sırada yazılmalıdır.
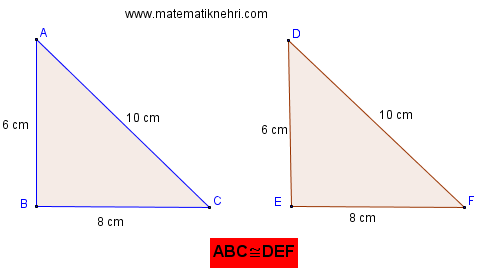
Yukarıdaki iki üçgenin Karşılıklı olarak kenar uzunlukları eşit olduğu için bu üçgenler eş üçgenlerdir.
Önemli Bilgi:
Üçgenlerde Eşlik bağıntısını göstermek için Aşağıdaki yöntemi kullanabilirsiniz.
1)ABC ≅ DEF deniyorsa;
# 1.sırada yazılan açı, karşı tarafta birinci sırada yazılan açıya eşittir. Aynı şekilde 2. Ve 3. Açılar içinde geçerlidir. Üstteki Eşlik bağıntısına göre;
s(A) = s(D)
s(B) = s(E)
s(C) = s(F) olur.
2) ABC ≅ DEF deniyorsa;
# ilk 2 sırada yazılan kenar uzunluğu, karşı tarafta yazılan ilk 2 sıradaki kenar uzunluğuna eşittir. Aynı şekilde Son iki sırada yazılan kenar uzunlukları eşittir. 1. Ve 3. Sırada yazılan kenar uzunlukları da birbirlerine eşittir. Üstteki eşlik bağıntısına göre;
|AB| = |DE|
|BC| = |EF|
|AC| = |DF| olur.
NOT: Eş Üçgenlerin Çevre Uzunlukları ve Alanları birbirlerine eşittir.
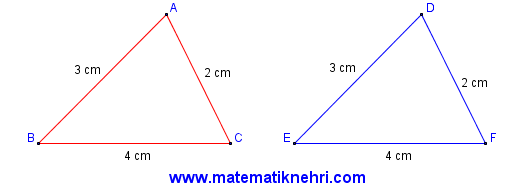
Örnek: Aşağıdaki Üçgenler Eş üçgenler midir?
Çözüm:
IABI = IDEI = 3 cm
IBCI = IEFI = 4 cm
IACI = IDFI = 2 cm olduğundan
ABC ≅ DEF olur.
ÜÇGENLERDE BENZERLİK
# İki üçgenin karşılıklı açılarının ölçüleri birbirine eşit ve karşılıklı kenarlarının uzunlukları orantılı ise bu üçgenler benzer üçgenlerdir.
# İki üçgenin benzerliğini “∼” sembolü ile gösteririz. Sembolle gösterirken eş olan açıları aynı sırada yazarız.
# Benzer iki üçgende karşılıklı kenarları oranlarsak bu oranlar bir sayıya eşit olur. Bu sayıya benzerlik oranı denir. Benzerlik oranını k harfi ile gösteririz.
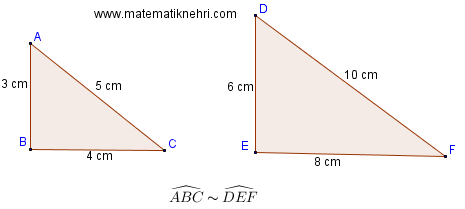
Yukarıda Açıları eşit olan Üçgenler verilmiştir.
s(A) = s(D)
s(B) = s(E)
s(C) = s(F)
Eş açıların karşılarındaki kenar uzunlukları orantılı olduğu için bu iki üçgen benzer üçgendir.
Kenar uzunluklarını oranlarsak;
‘’k’’ sayısına Benzerlik Oranı denir.
# Örnekte benzerlik oranı 1/2’dir. Pay ve paydaların yeri değişirse benzerlik oranı 2 olarak da yazılabilir.
Bu, “DEF üçgeninin kenar uzunlukları ABC üçgeninin 2 katıdır.” veya “ABC üçgeninin kenar uzunlukları DEF üçgeninin yarısıdır.” anlamına gelir.
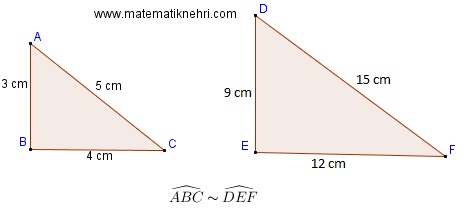
Örnek: Aşağıdaki Üçgenler birbirlerine benzer midir bulalım.
Kenarları birbirleriyle oranlayalım.
Üçgenlerin kenar uzunlukları oranı birbirlerine eşittir.
Bu nedenle benzerdirler ve ABC ≈ DEF olarak gösterilir.
Önemli Bilgi:
Üçgenlerde Eşlik bağıntısını göstermek için Aşağıdaki yöntemi kullanabilirsiniz.
ABC ∼ DEF deniyorsa;
# 1.sırada yazılan açı, karşı tarafta birinci sırada yazılan açıya eşittir. Aynı şekilde 2. Ve 3. Açılar içinde geçerlidir. Üstteki Benzerlik bağıntısına göre;
s(A) = s(D)
s(B) = s(E)
s(C) = s(F) olur.
2. ABC∼DEF deniyorsa;
# ilk 2 sırada yazılan kenar uzunluğu, karşı tarafta yazılan ilk 2 sıradaki kenar uzunluğuna oranı, Aynı şekilde Son iki sırada yazılan kenar uzunlukları oran ve aynı şekilde 1. Ve 3. Sırada yazılan kenar uzunlukları oranlarıda birbirlerine eşittir. Üstteki benzerlik bağıntısına göre;
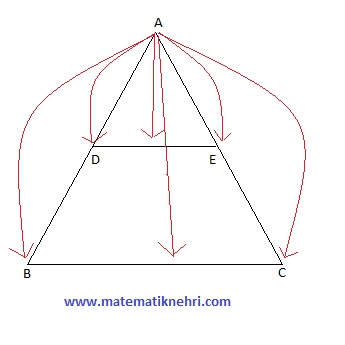
Temek Benzerlik Teoremi
Yukarıdaki üçgende DE//BC olmak şartıyla
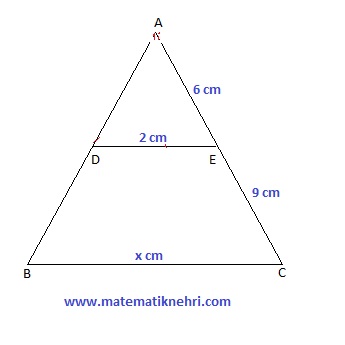
Örnek: DE//BC olduğuna göre x kaç cm dir?
EŞLİK VE BENZERLİK İLE İLGİLİ ÖZELLİKLER
# Her Eş Üçgen aynı zamanda benzerdir, ancak her benzer üçgen eş olmak zorunda değildir.
# İki üçgenin benzerlik oranı; çevre uzunluklarının oranına eşittir.
# İki üçgenin benzerlik oranı; yükseklikleri, açıortayları, kenarortayları oranına eşittir.
# İki üçgenin Alanları oranı; Benzerlik Oranının karesine eşittir.